В современной начальной школе таблицу умножения начинают учить во втором классе и заканчивают в третьем, причем часто выучить таблицу умножения задают на лето. Если же летом таблицей умножения вы не занимались, и до сих пор ребенок «плавает» в примерах на умножение, расскажем, как выучить таблицу умножения быстро и весело — с помощью рисунков, игр и даже пальцев рук.

Проблемы, которые часто возникают у детей в связи с таблицей умножения:
Язык умножения
Прежде чем начать учить вместе с ребенком таблицу умножения, стоит отойти немного в сторону и осознать, что простой пример на умножение можно описать удивительным количеством разных способов. Возьмите пример 3 × 4. Можно прочитать его как:
- трижды четыре (или четырежды три);
- три раза по четыре;
- три умножить на четыре;
- произведение трех и четырех.
Поначалу ребенку далеко не очевидно, что все эти фразы означают умножение. Вы можете помочь сыну или дочери, если, вместо того чтобы повторяться, будете как бы между прочим использовать разный язык в разговорах об умножении. К примеру: «Так сколько будет трижды четыре? Что получится, если взять три раза по четыре?»
В каком порядке учить таблицу умножения
Наиболее естественный для детей способ выучить таблицу умножения состоит в том, чтобы начать с самого простого и постепенно двигаться к самому сложному. Разумна такая последовательность:
Умножение на десять (10, 20, 30…), которое дети усваивают естественно в процессе обучения счету.
Умножение на пять (все-таки у всех нас по пять пальцев на руках и ногах).
Умножение на два. Пары, четные числа и удвоение знакомы даже маленьким детям.
Умножение на четыре (ведь это всего лишь удвоение умножения на два) и восемь (удвоение умножения на четыре).
Умножение на девять (для этого существуют достаточно удобные приемы, о них ниже).
Умножение на три и шесть.
Умножение на семь.
Почему 3×7 равно 7×3
Помогая ребенку выучить таблицу умножения, очень важно объяснить ему, что порядок чисел не имеет значения: 3 × 7 дает тот же ответ, что и 7 × 3. Один из лучших способов наглядно показать это — использовать массив. Это специальное математическое слово, обозначающее набор чисел или фигур, заключенный в прямоугольник. Вот, к примеру, массив из трех строк и семи столбцов.
*******
*******
*******
Массив — простое и визуальное средство помочь ребенку разобраться в том, как работают умножение и дроби. Сколько всего точек в прямоугольнике 3 на 7? Три строки по семь элементов насчитывают 21 элемент. Иными словами, массивы — доступный для понимания способ наглядно представить умножение, в данном случае 3 × 7 = 21.
Что, если мы нарисуем массив другим способом?
***
***
***
***
***
***
***
Очевидно, что в обоих массивах должно быть одинаковое число точек (их не обязательно при этом считать поштучно), поскольку, если первый массив повернуть на четверть оборота, он будет выглядеть в точности как второй.
Оглядитесь, поищите рядом, в доме или на улице, какие-нибудь массивы. Взгляните, к примеру, на пирожные в коробке. Пирожные уложены в массив 4 на 3. А если повернуть? Тогда 3 на 4.
А теперь взгляните на окна многоэтажки. Вот это да, это тоже массив, 5 на 4! А может быть, 4 на 5, как посмотреть? Стоит начать обращать внимание на массивы, как выяснится, что они всюду.
Как уполовинить таблицу умножения
Если вы уже усвоили с детьми идею о том, что 3 × 7 — это то же самое, что 7 × 3, то число фактов умножения, которые вам необходимо запомнить, резко уменьшается. Стоит заучить 3 × 7 — и в качестве бонуса вы получаете ответ на 7 × 3.
Знание переместительного закона умножения снижает число фактов умножения со 100 до 55 (не ровно наполовину из-за случаев возведения в квадрат, таких как 3 × 3 или 7 × 7, которые не имеют пары).
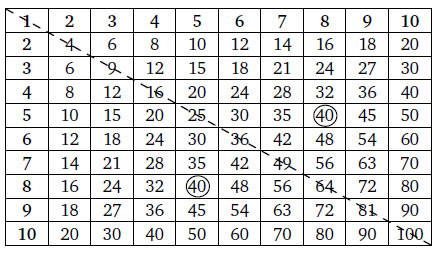
Каждое из чисел, расположенных выше пунктирной диагонали (к примеру, 5 × 8 = 40), присутствует и ниже нее (8 × 5 = 40).
Приведенная таблица содержит и еще одну подсказку. Дети обычно начинают учить таблицу умножения при помощи счетных алгоритмов. Чтобы сообразить, чему равно 8 × 4, они считают так: 4, 8, 12, 16, 20, 24, 28, 32. Но если ты знаешь, что восемью четыре — то же самое, что четырежды восемь, то 8, 16, 24, 32 будет быстрее. В Японии детей специально учат «ставить меньшее число первым». Семь раз по 3? Не делайте так, считайте лучше 3 раза по 7.
Заучивание квадратов чисел
Результат умножения числа на само себя (1 × 1, 2 × 2, 3 × 3 и т. д.) известен как квадрат числа. Это потому, что графически такое умножение соответствует квадратному массиву. Если вы вернетесь к таблице умножения и посмотрите на ее диагональ, то увидите, что всю ее составляют квадраты чисел.
У них есть интересная особенность, которую вы можете исследовать вместе с ребенком. Перечисляя квадраты чисел, обратите внимание, на сколько они каждый раз увеличиваются:
Квадраты чисел 0 1 4 9 16 25 36 49…
Разность 1 3 5 7 9 11 13
Эта любопытная связь между квадратами чисел и нечетными числами — прекрасный пример того, как разные виды чисел связаны между собой в математике.
Таблица умножения на 5 и 10
Первая и самая простая таблица, которую следует заучить — таблица умножения на 10: 10, 20, 30, 40…
Кроме того, дети относительно легко заучивают таблицу умножения на пять, и помогают им в этом руки и ноги, наглядно представляющие четыре пятерки.
Удобно также, что числа в таблице умножения на пять всегда заканчиваются на 5 или 0. (Так, мы точно знаем, что число 3 451 254 947 815 присутствует в таблице умножения на пять, хотя и не сможем в этом убедиться с помощью калькулятора: на экране устройства такое число просто не поместится).
Таблица умножения на 2, 4 и 8
Дети легко удваивают числа. Вероятно, это связано с наличием у нас двух рук по пять пальцев на каждой. Однако дети не всегда связывают удвоение с умножением на два. Ребенок может знать, что, если удвоить шесть, получится 12, но когда вы спрашиваете его, чему равно шестью два, ему приходится считать: 2, 4, 6, 8, 10, 12. В таком случае следует напомнить ему, что шестью два — то же самое, что дважды шесть, а дважды шесть — это и есть удвоенная шестерка.
Таким образом, если ваш ребенок хорошо удваивает, то он, по существу, знает таблицу умножения на два. При этом он вряд ли сразу сообразит, что с ее помощью можно быстро представить себе таблицу умножения на четыре — для этого нужно всего лишь удвоить и еще раз удвоить.

Игра: двойная бродилка
Можно приспособить любую игру, в которой игроки бросают кубик, таким образом, чтобы все броски считались двойными. Это дает сразу несколько преимуществ: с одной стороны, детям нравится идея пройти с каждым броском вдвое дальше, чем показывает кубик; с другой — они постепенно осваивают таблицу умножения на два. Кроме того (что немаловажно для родителей, занятых другими делами), игра заканчивается вдвое быстрее.
Таблица умножения на 9: метод компенсации
Один из способов освоить таблицу умножения на девять состоит в том, чтобы взять результат умножения на десять и вычесть лишнее.
Чему равно девять раз по семь? Десять раз по семь — это 70, вычитаем семь, получаем 63.
7 × 9 = (7 × 10) — 7 = 63
Возможно, быстрый набросок соответствующего массива поможет закрепить эту идею в сознании ребенка.
Если вы заучили таблицу умножения на девять только до «девятью десять», то девятью 25 поставит вас в тупик. Но десять раз по 25 это 250, вычитаем 25, получаем 225. 9 × 25 = 225.
Проверьте себя
Сможете ли вы решить пример 9 × 78 в уме методом компенсации (умножив на 10 и отняв 78)?
Учим таблицу умножения на 9 на пальцах
Существует и другой удобный способ освоить таблицу умножения на девять. В нем используются пальцы, а дети обожают это.
Держите руки перед собой ладонями вниз. Представьте, что ваши пальцы (включая и большой) пронумерованы от 1 до 10. 1 — мизинец на левой руке (крайний палец слева от вас), 10 — мизинец на правой (крайний палец справа).
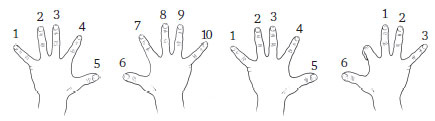
Чтобы умножить какое-то число на девять, загните палец с соответствующим номером. Скажем, вас интересует девятью 7. Загните палец, который вы мысленно обозначили как седьмой номер.
А теперь взгляните на свои руки: число пальцев слева от загнутого даст вам число десятков в ответе; в данном случае это 60. Количество пальцев справа даст число единиц: три. Итог: 9 × 7 = 63. Попробуйте: этот метод работает со всеми однозначными числами.
Таблица умножения на 3 и на 6
Для детей таблица умножения на три — одна из самых сложных. В данном случае практически не существует никаких приемов, и таблицу умножения на 3 придется просто вызубрить.
Таблица умножения на шесть следует непосредственно из таблицы умножения на три; здесь, опять же, все сводится к удвоению. Если умеешь умножать на три, просто удвойте результат — и получите умножение на шесть. Таким образом, 3 × 7 = 21, 6 × 7 = 42.
Таблица умножения на 7 — игра в кости
Итак, все, что у нас осталось, — таблица умножения на семь. Есть хорошая новость. Если ваш ребенок успешно овладел таблицами, описанными выше, нет нужды вообще ничего заучивать: все уже есть в остальных таблицах.
Но если ваш ребенок захочет выучить таблицу умножения на 7 отдельно, мы познакомим вас с игрой, которая поможет ускорить этот процесс.
Вам потребуется столько игральных кубиков, сколько сможете найти. Десять, к примеру, — отличное количество. Скажите сыну или дочери, что хотите посмотреть, кто из вас сможет быстрее сложить выпавшие на кубиках числа. Однако позвольте детям самим решить, сколько кубиков бросать. А чтобы повысить шансы ребенка на выигрыш, можете договориться, что тот должен сложить числа, указанные на верхних гранях кубиков, а вы — те, что и на верхних, и на нижних.
Пусть каждый ребенок выберет по крайней мере два кубика и положит их в стакан или кружку (в них удобно трясти кости, добиваясь случайности броска). Вам нужно знать лишь, сколько кубиков взял ребенок.
Как только кубики брошены, вы можете сразу же посчитать, какую сумму дадут числа на верхних и нижних гранях! Каким образом? Очень просто: умножив число кубиков на 7. Таким образом, если было взято три кубика, сумма верхних и нижних чисел составит 21. (Причина, разумеется, в том, что числа на противоположных гранях игральной кости всегда дают в сумме семь.)
Дети будут так поражены скоростью ваших подсчетов, что тоже захотят овладеть этим методом, чтобы когда-нибудь воспользоваться им в игре с приятелями.
Таблица умножения на 12
В эпоху так называемой Британской имперской системы мер и «недесятичных» денег каждому необходимо было владеть счетом до 12 × 12 (тогда в шиллинге было 12 пенсов, а в футе 12 дюймов). Но и сегодня 12 то и дело всплывает в расчетах: множество людей по-прежнему меряет и считает в дюймах (в Америке это стандарт), а яйца продают дюжинами и полудюжинами.
Мало того. У ребенка, свободно перемножающего числа больше десяти, начинает вырабатываться понимание того, как перемножаются большие числа. Знание таблиц умножения на 11 и 12 помогает заметить интересные закономерности. Приведем полную таблицу умножения до 12.
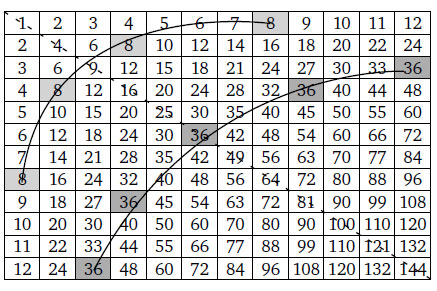
Обратите внимание: число восемь, к примеру, встречается в таблице четыре раза, тогда как 36 — пять раз. Если соединить все ячейки с числом восемь, получится плавная кривая. То же можно сказать и про ячейки с числом 36. В самом деле, если какое-то число появляется в таблице больше двух раз, то все места его появления можно соединить плавной кривой примерно одинаковой формы.
Вы можете подтолкнуть своего ребенка к самостоятельному исследованию, которое займет его (может быть) на полчаса, а то и больше. Распечатайте несколько экземпляров таблицы умножения двенадцати первых чисел на 12, а затем попросите его сделать следующее:
- раскрасить все ячейки с четными числами красным цветом, а с нечетными — синим;
- определить, какие числа встречаются там чаще всего;
- сказать, сколько в таблице встречается различных чисел;
- ответить на вопросы: «Какое самое маленькое число не встречается в этой таблице? Какие еще числа от 1 до 100 в ней отсутствуют?».
Фокус с одиннадцатью
Таблица умножения на 11 строится проще всего.
1 × 11 = 11
2 × 11 = 22
3 × 11 = 33
4 × 11 = 44
5 × 11 = 55
6 × 11 = 66
7 × 11 = 77
8 × 11 = 88
9 × 11 = 99
Но что же дальше? Есть очень симпатичный простой прием, позволяющий без труда умножить любое число от 10 до 99 на 11:
- Возьмите любое число от десяти до 99 — пусть это будет, скажем, 26.
- Разбейте его на два числа и раздвиньте их, чтобы в середине образовался пробел: 2 _ 6.
- Сложите между собой две цифры вашего числа. 2 + 6 = 8 и вставьте то, что получилось, в середину: 2 8 6
Это ответ! 26 × 11 = 286.
Но будьте осторожны. Что получится, если вы перемножите 75 × 11?
- Разбиваем число: 7 _ 5
- Складываем: 7 + 5 = 12
- Вставляем результат в середину и получаем 7125, что очевидно неверно!
В чем дело? В этом примере есть небольшая хитрость, которую нужно применять тогда, когда цифры, использующиеся для обозначения числа, в сумме дают десять или больше (7 + 5 = 12). Прибавляем один к первой из наших цифр. Следовательно, 75 × 11 будет не 7125, а (7 + 1)25, или 825. Так что фокус на самом деле не так прост, как может показаться.
Игра: победи калькулятор
Цель этой игры — развить навык быстрого пользования таблицей умножения. Вам потребуется колода игральных карт без картинок и калькулятор. Решите, кто из играющих первым будет использовать калькулятор.
Правила:
- Игрок с калькулятором должен перемножить два выпавших на картах числа; при этом он должен использовать калькулятор, даже если знает ответ (да, это может быть очень тяжело).
- Другой играющий должен перемножить те же два числа в уме.
- Тому, кто получает ответ первым, достается очко.
- После десяти попыток игроки меняются местами.










Add Comment